
트리구조란?
트리구조는 노드가 부모와 자식의 관계를 갖고 있는 비선형 자료구조. (뒤집힌 나무)
선형구조로는 큐,스택,연결리스트가 있다.
(head를 root라고 보고 세로로 세운다면 연결리스트와 유사하다 [물론 부모와 자식을 갖고 있다는 점을 제외하면 .ㅎ])


2. 일상생활에서 볼 수 있는 트리구조
트리구조는 우리가 일상에서 많이 접할 수 있는 구조이다.
위에 사진들처럼 대진표에서도 볼 수 있고 회사의 조직도, 가족의 구성원을 트리 구조로 한 가계도
그리고 Html 역시 트리구조이다.

depth와 height, level은 어떻게 다른가요?
depth는 트리 중 가장 긴 경로의 간선 개수를 말한다.
(A에서 H까지의 depth는 ? [A->B. B->D. D->H ] // 3)
height는 루트에서 특정 노드 사이의 간선 개수를 말한다.
(A에서 F까지의 height는? [A->C, C->F] // 2 )
level은 깊이와 정의가 비슷하지만 간선의 개수가 아닌 노드의 개수를 말한다.
(A에서 H까지의 level은? [A,B,C,D] // 4)


트리와 그래프의 차이점은 무엇인가요?
트리는 그래프의 종류 중 하나이다.
트리가 갖고 있는 가장 큰 특징은 노드가 부모와 자식의 관계를 갖고 있다는 점이다.
트리가 그래프의 종류 중 하나 이지만 둘의 가장 큰 차이점 트리는 형제관계에서 노드를 연결할 수 없다는 점이다.
(물론 자료들이 부모와 자식의 구조를 갖는다는 것 역시)
3. 이진트리의 종류.


Ternary tree => 부모 노드가 갖을 수 있는 자식의 노드 개수에 제한이 없는 트리구조.(이진트리 아님)
Binary tree => 부모의 노드가 갖을 수 있는 최대 자식 노드 수는 2개로 제한되어 있는 트리구조.
Binary search tree
=> 부모의 노드가 갖을 수 있는 최대 자식노드가 2개이며
부모노드를 기준으로 왼쪽은 부모의 키 값보다 작으며 부모노드의 오른쪽으로는 부모노드의 값보다 커야 한다.
[중위순회를 했을 시 값이 내림차순된다.]
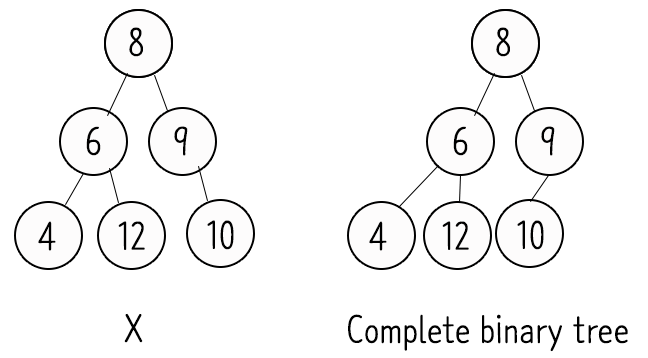


Complete binary tree => 마지막 레벨을 제외한 모든 서브트리의 레벨이 갖아야 하고, 마지막 레벨은 왼쪽부터 채워야 하는 트리.
Full binary tree => 자식 노드가 아예 없거나, 두개를 갖고 있어야 하는 트리.
Perfect binary tree => 완벽한 피라미드 구조로 빈 공간이 없고 루트를 제외한 모든 노드가 자식을 2개씩 갖고 있어야는 트리.
4. 트리의 순회방법.

1. Inorder(중위순회) => Left -> Root -> Right
[4,2,5,6,1,7,3,8]
2. Preorder(전위순회) => Root -> Left -> Right
[1,2,4,5,6,3,7,8]
3. Postorder(후위순회) => Left -> Right -> Root
[4,6,5,2,7,8,3,1]
트리구조에 밸런스가 깨지면 어떻게 될까?

밸런스가 깨져버리면,,,연결리스트가 되어버린다.
그렇기에 트리구조를 구현할 할 때 밸런스를 맞출 수 있도록 구현을 해야한다.
'2020-2021 > TIL' 카테고리의 다른 글
| Instantiation Patterns (0) | 2020.10.28 |
|---|---|
| Obj Oriented Programming?! (0) | 2020.10.28 |
| 26일 HashTable (0) | 2020.10.26 |
| 10월23일 Linked List (0) | 2020.10.23 |
| 10월 22일 stack&queue (0) | 2020.10.22 |




댓글